.... FÍSICA DE PARTÍCULAS - EL ESPACIO TIEMPO FRACTAL

Para la Ciencia Clásica, el universo se puede modelar con la geometría euclideana. Sin embargo, ahora se sabe que la naturaleza favorece el CAOS y no la "perfección", ya que ese caos es el que permite la aparición de sistemas físicos y biológicos viables. Por ejemplo, los alveolos siguen una "distribución fractal finita" que resuelve de una manera elegante y eficiente el problema ingenieril sobre como presentar la mayor área expuesta dentro del menor volumen posible (al igual que la corteza cerebral).
Cuando Riemann demostró que la geometría sólo es una creación mental y arbitraria, las matemáticas se tambalearon y comenzó el estudio de nuevos tipos de geometría:
* Geometría Esférica (curvatura positiva): donde dos líneas paralelas terminan cortándose
* Geometría Hiperbólica (curvatura negativa): donde dos líneas paralelas cada vez se separan más, etc.

Esta nueva geometría "curvada" (junto con los trabajos de Minkowski, Lobachevsky y otros) se convirtió en el fundamento de la Teoría de la Relatividad, donde muchos de los fenómenos "anti-clásicos" son simples consecuencias de las distorsiones sufridas por el EspacioTiempo.

En 1904, el Matemático Helge von Koch dio a conocer una curva matemáticamente "imposible": - En esta curva no es posible trazar una tangente en ningún punto de su perímetro - La longitud entre dos puntos de su perímetro es infinita - La curva encierra un área finita La curva de von Koch presenta las mismas características que la costa de una isla. Luego, es correcto afirmar que "la longitud de la costa de Inglaterra es infinita". Si no lo parece es por la RESOLUCIÓN utilizada, es decir, el perímetro depende de la escala en la que se trabaje. La curva de von Koch demostró que todas las ciencias euclideanas y cartesianas tenían cimientos muy frágiles y comenzaron a constatarse grietas en el edificio de la ciencia.

"Monstruo de von Koch"

Luego, surgieron cuestionamientos lógicos:
- Según Euclides, una línea es una sucesión de puntos. ¿Es posible que un objeto de 0 Dimensiones pueda dar origen a un objeto de 1 Dimensión?
- Los trabajos de Gödel, Turing y otros permitieron trabajar con nuevos sistemas lógicos donde la negación de la negación no es necesariamente la afirmación (Lógica Difusa). Por ejemplo: Un peluquero le corta el pelo sólo a aquellos que no se cortan el pelo a sí mismos. Pregunta: ¿El peluquero se corta el pelo a sí mismo?. O también: ¿Se puede demostrar que una serie temporal con una gran dispersión no ha sido generada por una función específica? Otro enigma difuso: si un Rey ordena que le desobedezcan, ¿al ser desobedecido realmente está siendo obedecido?

Los fractales regulares son figuras geométricas autosimilares frente a cambios de escala:

Presentan estructura fractal: - Los copos de nieve - La costa de una playa - Los alveolos - Una brócoli - Las dendritas de las neuronas - Los helechos - Un imán - Un cristal - Ondas cerebrales "sanas", etc.

Mandalas dentro de Mandalas (fractal irregular)

El concepto de fractal regular se puede generalizar a "entidades" autosimilares. Existen ecuaciones, algoritmos, funciones, etc. con comportamientos autosimilares como los sistemas "Depredador-Presa". Las irregularidades peculiares de muchos fenómenos se mantienen frente a cambios de escala. Es decir, las irregularidades pueden ser REGULARES, o en otras palabras, PUEDE HABER ORDEN DENTRO DEL CAOS.

Debido a convenciones culturales pocas personas se percatan de la subjetividad de la geometría. Por ejemplo, si se pidiera una lista con objetos 1D, 2D y 3D las respuestas podrían ser del siguiente tipo:
- 1D: una cuerda
- 2D: la hoja de un libro
- 3D: una manzana
La verdad es que la cuerda es aproximadamente cilíndrica (3D) y la hoja del libro tiene un espesor (3D también). Es más: desde lejos, la hoja de un libro puede parecer un punto (0D). ¿Cómo dar cuenta de estos hechos?

DIMENSIÓN FRACTAL, DE HOMOTECIA O DE AUTOSIMILITUD
La dimensión fractal de una entidad cualquiera puede determinarse del siguiente modo:

Ejemplos:
i) Para una recta formada por N= 3 segmentos:

ii) Para un cuadrado formado por N= 9 "baldosas":

iii) Para una sección de la curva de von Koch después de la primera iteración:

(el término fractal fue acuñado por Mandelbrot y proviene de los vocablos fracture, fraction y frangere (romper))

Por otro lado, el perímetro de cualquier sección de la curva de von Koch es infinita:

Cabe señalar que una figura determinada puede tener una dimensión fractal dependiente de la escala o resolución en la que se realizó el cálculo. Por ejemplo, una línea que se tomó como recta (D= 1) vista con más detalle puede presentar espesor e irregularidades (D> 1). Uno de los fractales más estudiados corresponde al Conjunto de Julia y uno de sus elementos se puede obtener con la siguiente fórmula recursiva en el plano complejo: . El resultado depende de la semilla utilizada. Por ejemplo, Z0= 1.05 + 0.3i produce una órbita finita en el plano complejo.

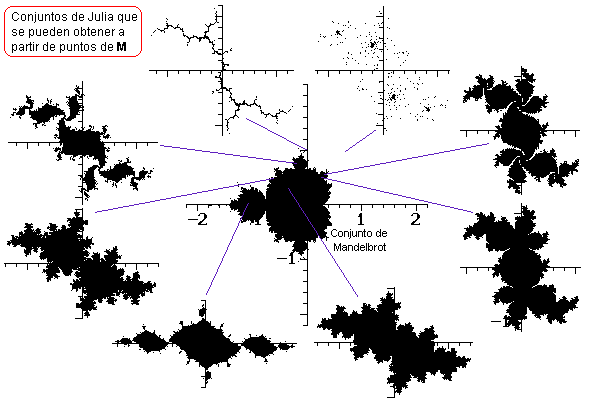LA BÚSQUEDA DE COMPRESIONES
La presencia de irregularidades regulares nos puede llevar a pensar en la posibilidad de "comprimir" muchos fenómenos en una pequeña fórmula o, equivalentemente, de crear una simulación de una dimensión menor que la original para representarlo. Un sinnúmero de pruebas psicológicas ha demostrado que nuestra mente tiende a buscar (desesperadamente) cualquier regularidad o patrón como substrato para anclar ideas y/o percepciones (Test de Rörschach). ¿Cuál será la ventaja selectiva de esta "manía"? Difícilmente puede comprenderse cómo es posible almacenar una gran cantidad de información no redundante en una dimensión menor que la original...

PISTAS
* Se puede utilizar una fórmula que se expanda a sí misma (como los "autómatas celulares"):
* Se puede estar trabajando con una serie temporal extraña y calcular la dimensión fractal a la cual los "falsos vecinos" comienzan a ser cero. Si por ejemplo D= 4.3, significa que la serie se puede reducir a una simulación de 4.3 dimensiones. Es decir, la función que comprime la serie puede depender de cinco variables.
* Se puede almacenar información binaria en un "spin glass" (molécula especial 3D). Si ese spin glass se coloca justo en el horizonte de un agujero negro, pasará a tener 2 dimensiones, pero la información se mantendrá incólume. Tal vez no sea tan irracional la posibilidad de "tener el universo comprimido en un grano de arena".
* En un "fractal regular" (o totalmente autosimilar frente a cambios de escala) se tiene que la parte contiene al todo: 1 cm² del plano complejo contiene la misma figura fractal que se puede observar en 1 Km² de éste. Algo parecido ocurre con los hologramas, donde cada parte tiene la propiedad de poder reproducir por sí sola a la imagen completa.

CONCLUSIÓN
La ciencia se puede definir como la búsqueda de compresiones. Siempre se pretende explicar un fenómeno que ocurre en N dimensiones por intermedio de una simulación de M < N dimensiones. Y esta es la Teoría de Todas las Cosas (o del Campo Unificado). Allí tenemos que se pretende reducir las cuatro fuerzas del universo a una única "fuerza unificada". Por otro lado, si en un caso particular no se consigue la compresión (o si no es práctica o "computable"), se utilizarán herramientas estadísticas como en el caso de predecir cómo caerá un dado (a pesar de ser un fenómeno 100% determinista). De acuerdo con los trabajos de Gödel y Chaitin, no es posible probar que una compresión no se pueda comprimir aún más. Siempre estará abierta la posibilidad de encontrar una unificación aún más profunda y simple. A modo de ejemplo, consideremos:

El escuchar la música, ver la evolución de una variable física y apreciar una fotografía equivale a definir un conjunto "por extensión". ¿Será posible expresarlos por comprensión? ¿Existirá alguna forma abreviada de comprimir la información inicial en una simulación de menor dimensión que la original?
"Evidentemente" ni la música, ni una serie temporal, ni una fotografía se pueden expresar por comprensión. En los tres casos, la información no se puede reducir a una dimensión menor (¿o sí?). Sin embargo, como las mentes humanas presentan la manía de querer "etiquetar" todo para comprenderlo, seguramente nos sentiremos satisfechos especificando parámetros estadísticos: promedios, cuartiles, desviación estándar, moda, mínimo y máximo, espectro de frecuencias, etc. Parece lógico, ¿verdad? Pues bien, los tres ejemplos fueron generados por una fórmula. Toda la información de tres cosas aparentemente complejas se puede expresar con unos pocos Kb (en el caso de la imagen del esquiador, el archivo bmp pesa 1.15 Mb, el jpg pesa 270 Kb y el fractal que la genera pesa 20 Kb). Luego, ¿Qué nos garantiza que el enfoque estadístico para un fenómeno muy complejo sea el adecuado si puede existir una simple fórmula que lo genere?

El Espacio Tiempo Fractal
I) Relatividad Restringida (1905)
Esta teoría fusiona el Espacio y el Tiempo (en Sistemas Inerciales de Referencia, SIRs) debido al hecho demostrado de que la velocidad de la luz es independiente del observador. Las consecuencias se pueden deducir a partir de diagramas EspacioTemporales conocidos como "Líneas de Mundo" y son las siguientes:
- El espacio depende del observador
- El tiempo depende del observador
- La simultaneidad depende del observador
- Las líneas de mundo no pueden estar a más de 45°, debido a que esto significaría una violación del Principio de Causalidad (¿Es esto irracional en el fondo?)
- El "Intervalo EspacioTemporal" es un invariante:
(equivale a Pitágoras en el EspacioTiempo)

II) Relatividad General (1915)
Einstein generalizó la Relatividad Restringida para poder aplicarla en sistemas donde la gravedad curva el EspacioTiempo (en Sistemas Acelerados de Referencia). Aquí se observa que las líneas rectas asociadas a observadores "inerciales" se reemplazan por geodésicas, dado que en los SARs el EspacioTiempo no es plano. Las irregularidades presentes en el EspacioTiempo nos permiten especificar el movimiento de una forma "absoluta" respecto de esas irregularidades.

El EspacioTiempo 4D puede experimentar "agusanamientos" (según Wheeler), lo que viola la propiedad de "conexitud" exigido por los modelos FRW del Universo (plano, esférico e hipérbólico):

(Una superficie es conexa cuando toda curva cerrada puede convertirse en un punto de un modo continuo)

III) Mecánica Cuántica y Fractales (1925)
Inicialmente la MQ se formuló a "bajas" velocidades, pero en los años 30 se introdujo correcciones relativistas a la ecuación de Schrödinger para poder aplicarla a partículas microscópicas que viajan a velocidades altas. Consecuencias:
- Cada partícula se asocia con un campo y viceversa:

- Aparece el "Pincipio de Exclusión de Pauli" para partículas con espín semientero.

Además se descubre que el vacío no está realmente vacío, ya que debido al Principio de Incertidumbre de Heissenberg las partículas asociadas a los campos siempre están "vibrando", incluso en su estado fundamental. Esto significa que los campos siempre presentan fluctuaciones. Por lo tanto... ¿La densidad de energía del vacío es infinita?. Esto se evita con la "Teoría de Renormalización", donde aparecen energías de campo negativas (Efecto Casimir, 1948) que permiten llevar la energía a cero gracias al aporte de fotones térmicos.
Las fluctuaciones de curvatura requieren de un aporte de energía, de modo que el EspacioTiempo se opone a la curvatura (presenta "rigidez"). Las fluctuaciones cuánticas pueden excitar "paramétricamente" a las partículas asociadas a los campos, lo que provocará la aparición y desaparición de materia. La tasa de generación de partículas será mayor donde mayor sea la curvatura y su derivada (esto podría explicar la aparición de materia después del Big Bang). El que la curvatura del EspacioTiempo presente fluctuaciones cuánticas nos lleva a visualizarlo como un fractal cuando se observa en la escala adecuada:

Un objeto aparentemente 3D (como una barra de acero) presentará poros, de modo que realmente será un objeto de 2.x dimensiones. Así mismo, podemos visualizar el EspacioTiempo a escala subatómica como una "espuma":

Debido a esto, algunos Físicos piensan que la descripción del EspacioTiempo como un continuo uniforme (donde dx y dt se pueden hacer tender a cero indefinidamente) es inadecuada a pequeña escala, pero una buena aproximación a gran escala. Por lo tanto, las magnitudes físicas podrían depender de la escala o de la resolución utilizada... es decir, serían fractales....

IV) Dimensiones Enrrolladas
Kaluza y Klein consideraron en los años 20 que una dimensión del EspacioTiempo podía curvarse en un radio de un par de longitudes de Planck ( ~ 10^-35 m), por lo que esa dimensión sería indetectable para nosotros, ya que apenas comenzaramos a movernos en la dirección definida por esa dimensión, volveríamos inmediatamente al punto de partida. Más tarde, en los años 60, se resucitó la Teoría de Kaluza-Klein cuando los Físicos empezaron a trabajar en marcos EspacioTemporales con muchas dimensiones. En estas nuevas dimensiones curvadas también aparecen fluctuaciones, lo que genera partículas con tres espines posibles: . Pero si se une la Teoría de Kaluza-Klein con el supuesto de "Supersimetría", aparecen todos los espines existentes. La Supersimetría dice que a altas energías todo bosón de espín debe tener un "fermión partner"de espín (y viceversa). A partir de la Supersimetría se puede deducir que las leyes físicas deben ser las mismas para todos los observadores, lo que permite llegar a la teoría de la (SUPER-) Gravedad de Einstein. En este caso se tiene que la interacción gravitatoria es transmitida por el "gravitón" cuyo superamigo es el "gravitino" . Lamentablemente no se ha encontrado ningún superpartner por lo que se cree que de algún modo debe romperse esta simetría.
En 1978 Cremmer, Julia y Scherk comprendieron que la Supergravedad podía modelarse con el máximo de dimensiones posibles (11). Al ir curvando estas dimensiones se puede (en principio) derivar a partir de la Supergravedad, la fuerza electromagnética, la nuclear fuerte y la nuclear débil. He ahí el camino para conseguir una Teoría del Campo Unificado. A la Teoría Unificada en 11 dimensiones se le conoce como "Teoría M" o "Teoría de Todas las Cosas". Con mucho esfuerzo se ha conseguido desarrollar cinco teorías en 10 dimensiones (= supercuerdas) y además se sabe que es posible conseguir la unificación de estas cinco teorías al trabajar en 11 dimensiones (se sabe que se puede hacer, pero aún no se sabe cómo hacerlo). Las cinco teorías en diez dimensiones son:
- Tipo I
- Tipo IIA
- Tipo IIB
- Heterótica E₈xE₈
- Y Heterótica SO(32)

V) Relatividad de Escala y EspacioTiempo Fractal
No es necesario que una curva en el EspacioTiempo sea continua para garantizar su diferenciabilidad. Esta podría depender de la resolución:

Y así es como la Mecánica Cuántica puede deducirse a partir de una Teoría de la Relatividad donde el EspacioTiempo sea fractal ("espumoso") debido a las permanentes fluctuaciones cuánticas y dimensiones curvadas. Como la diferenciabilidad depende de la escala, se impone automáticamente la necesidad de utilizar una descripción probabilística para el mundo microscópico. Por lo tanto, todas las variables físicas pasan a depender de la escala y de las características geométricas de las geodésicas fractales. La descripción clásica surge al promediar mediante una función de onda todos los comportamientos posibles en un Espacio de Fase fractal:

En este marco es imposible saber qué trayectoria específica seguirá la partícula, porque el EspacioTiempo es "espumoso".

Además, la "Relatividad de Escala" permite conseguir la unificación simultánea de las cuatro fuerzas del universo en la "Energía de Planck" ( ~ 10¹⁸ GeV), que es precisamente la energía donde se sabe que la gravedad se vuelve tan intensa como las otras tres fuerzas:

FIN DE LA SERIE

Tema relacionado: Geofísica y Fractales | BUSCAR ARTICULOS

Home: www.geofisica.cl

REFERENCIAS
* "Abrazando el Universo (Física para Poetas)", Claudio Escobar Cáceres, Ediciones Plantar un árbol, escribir un folleto, tener una hija.
* Relatividad de Escala, Página Web de Laurent Nottale.
* Molecular Expressions: permite constatar visualmente la relación entre los fractales y la escala.
* "Curvas Fractales" y "Teoría del Caos", César Monroy Olivares. Editorial Alfaomega.
* Investigación y Ciencia. Diversos números. Artículos de Bryce S. DeWitt, Laurent Nottale y Luis Ibáñez, entre otros.
* El Universo Elegante. Excelente página de Física de Partículas y SuperCuerdas.